The Essence of the Law of Large Numbers

Law of Large Numbers — More Numbers More accuracy ( Statistical Stability ) DataMantra DataMantra — Image Source — Trade Brains

The Law of Large Numbers is a fundamental principle in statistics that describes the behavior of sample averages as the sample size increases. Simply put, as we collect more data, our estimates tend to get closer to the true population parameter.

It is a theorem that states that as the number of trials increases, the difference between the expected value and the actual value shrinks. But, Before we go for examples I love to touch base the History always.

The Italian mathematician Gerolamo Cardano (1501–1576) stated without proof that the accuracies of empirical statistics tend to improve with the number of trials.

This was then formalized as a law of large numbers. A special form of the LLN (for a binary random variable) was first proved by Jacob Bernoulli. It took him over 20 years to develop a sufficiently rigorous mathematical proof which was published in his Ars Conjectandi (The Art of Conjecturing) in 1713. He named this his “Golden Theorem” but it became generally known as “Bernoulli’s theorem”.

In 1837, S. D. Poisson a French statistician further described it under the name “la loi des grands nombres” (“the law of large numbers”).

After Bernoulli and Poisson published their efforts, other mathematicians also contributed to the refinement of the law, including Chebyshev, Markov, Borel, Cantelli, Kolmogorov, and Khinchin.

Markov further’s studies have given rise to two prominent forms of the LLN. One is called the “weak” law and the other the “strong” law.

Let’s quickly start with an example:

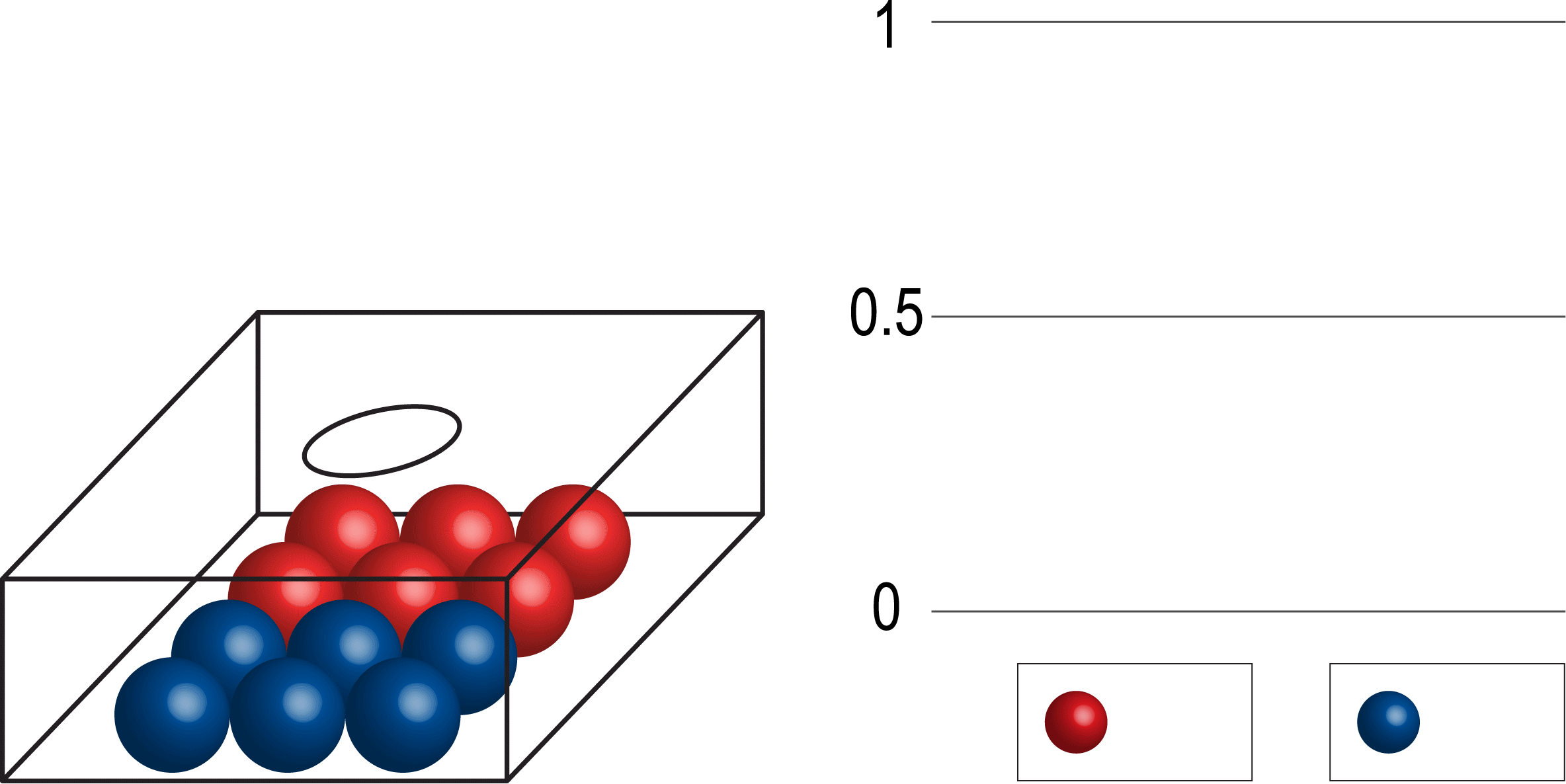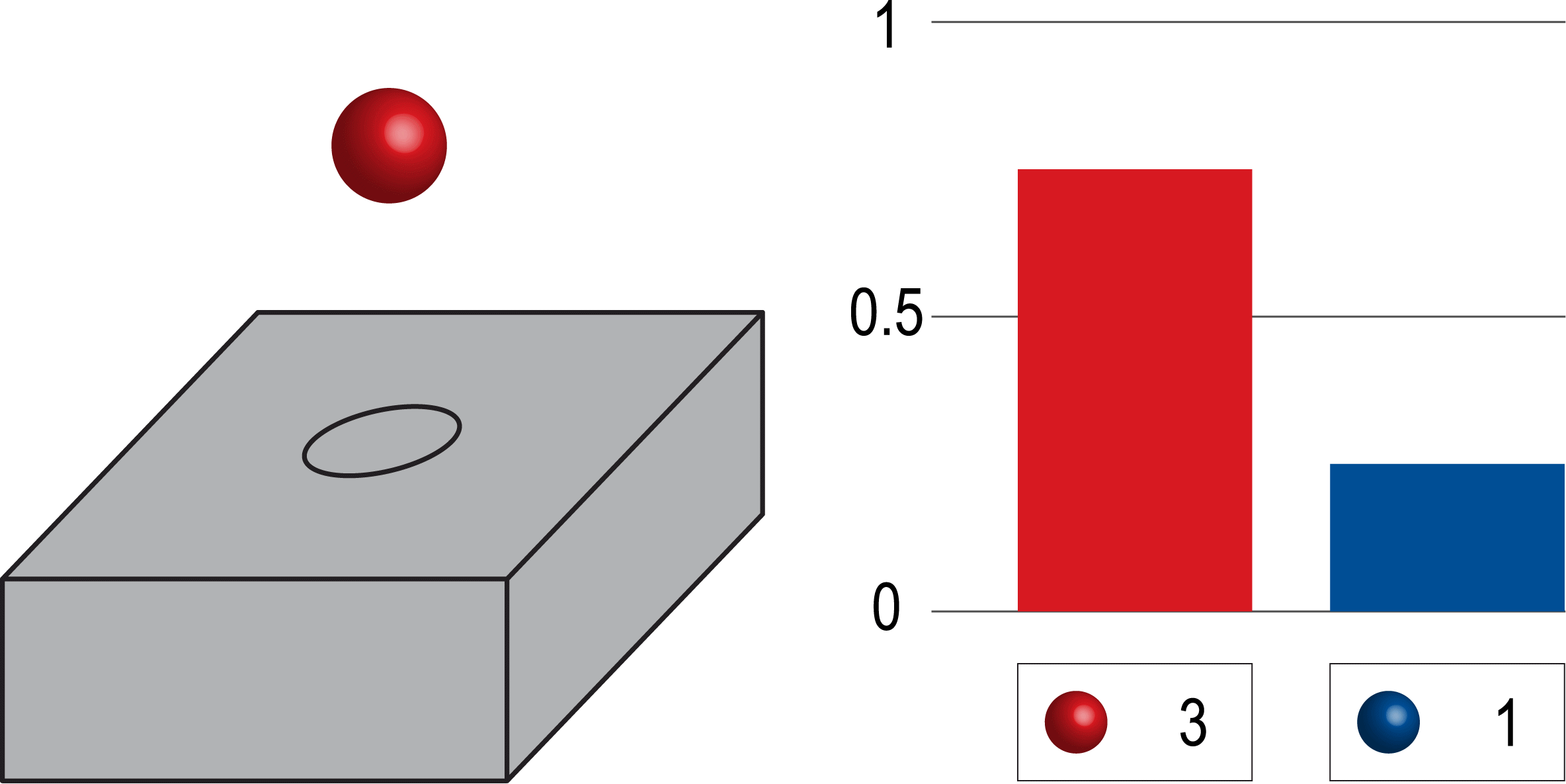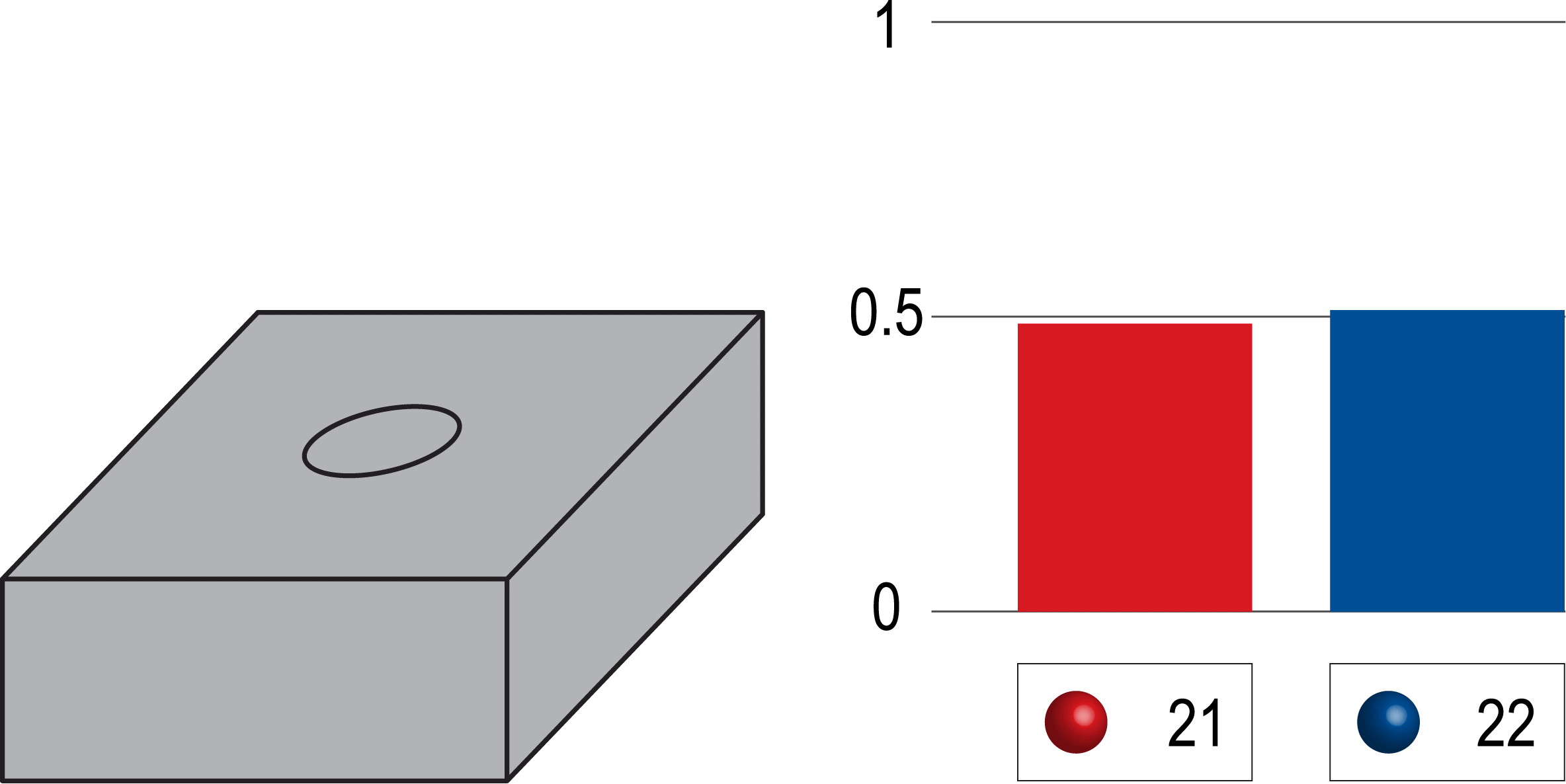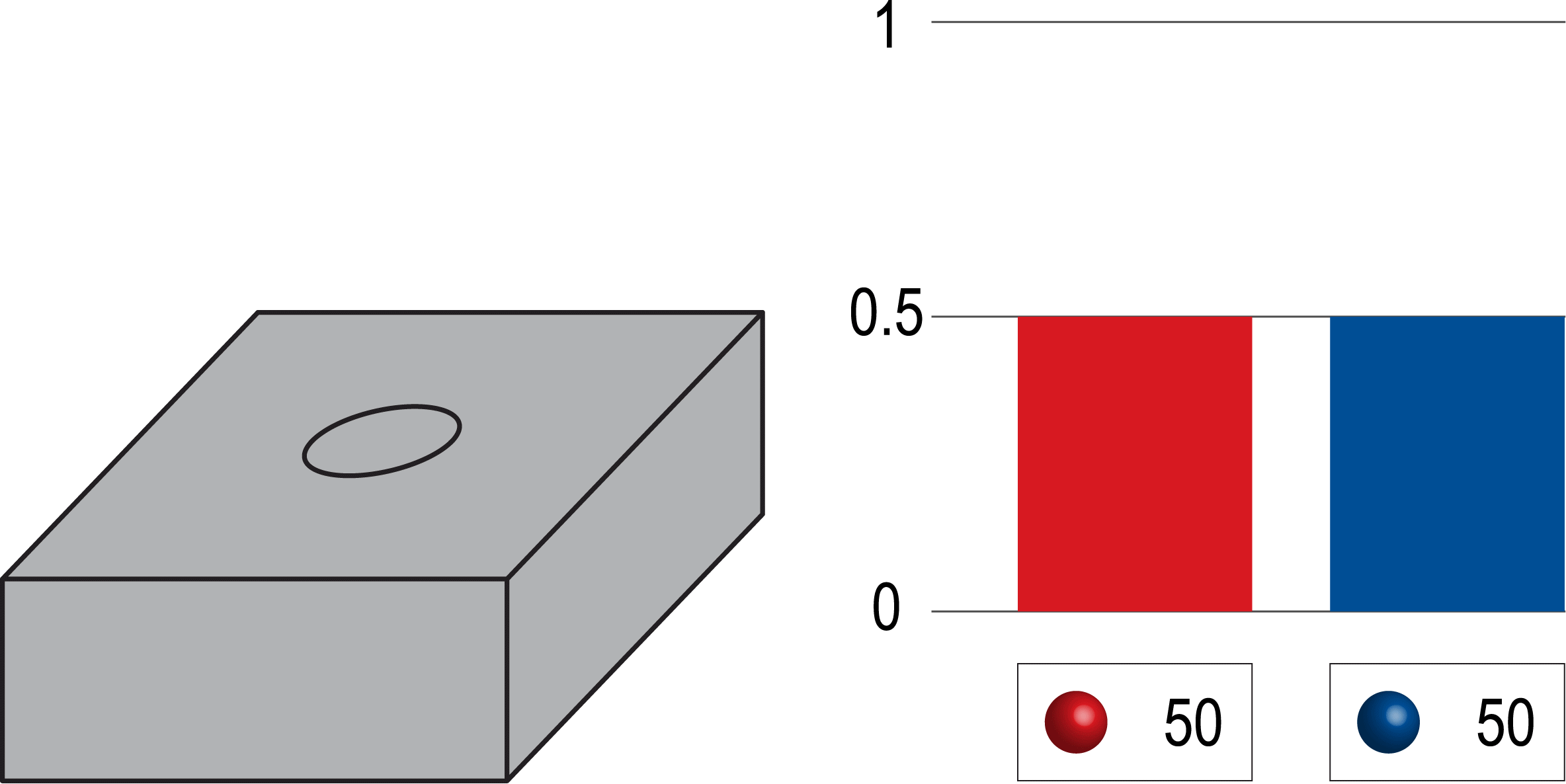
Think of it this way, if you have a bag full of blue and red marbles, and you keep picking marbles out of the bag one by one, the more marbles you pick, the closer you’ll get to having half of them be blue and half of them be red.

Even if you started by picking a bunch of blue marbles in a row, eventually, as you keep picking, the ratio of blue to red will start to even out.

So, in essence, the law of large numbers tells us that with a large enough sample size, the observed outcomes will more closely reflect the true underlying probabilities.

Hakuna Matata Meaning :-“As we increase the sample size the sample mean approaches the population mean’’The more data we have, the more reliable our estimates become.

Why It Matters?

The Law of Large Numbers is super important because it helps us make predictions and decisions based on data. When we’re looking at a big enough sample (like flipping a coin many times or picking lots of marbles out of a bag), we can trust that the results we get will reflect the true probabilities of the situation. So, it’s like saying the more data we have, the more reliable our conclusions will be.

It’s a bit like saying that the more you practice something, the better you’ll get at it. So, whether you’re flipping coins, rolling dice, or analyzing data, knowing about the Law of Large Numbers can help you understand how reliable your results are.

There are plenty of examples of this Law:

Example — 1:- Stocks

In Stocks, if an investor has a diversified portfolio of stocks, the risk of losing money decreases as the number of stocks in the portfolio increases. This is because the investor is less likely to have all of their stocks decline in value at the same time.

Example — 2:- Healthcare

In healthcare, the LLN is used to study the effectiveness of treatments. If you want to know whether a certain medication is effective for a particular condition, you could study a small sample of patients and get a rough idea. However, if you were to study a larger sample of patients, you would get a more accurate estimate of the effectiveness of the medication.

Don’t worry it takes time so here is my favorite Example:

Let’s consider the example of Exit polls in an election:

During an election, polling agencies often conduct exit polls to gauge voter preferences. These polls involve interviewing voters as they leave the polling stations to ask them about their choices.

Now, imagine a hypothetical scenario where there’s an election with two candidates, Candidate A and Candidate B. Let’s say that according to the opinion polls, Candidate A is expected to win 60% of the votes, while Candidate B is expected to win 40%.

If only a small number of voters are surveyed in exit polls, there’s a chance that the sample might not accurately represent the entire voting population.

For instance, the first few voters interviewed might disproportionately favor Candidate A, even if the overall electorate is evenly split.

However, as the number of voters surveyed in the exit polls increases, the law of large numbers comes into play. With a larger sample size, the proportion of voters favoring each candidate in the exit polls will tend to get closer to the expected 60–40 split.

This means that with a sufficiently large sample size, the exit polls are more likely to accurately reflect the actual voting patterns of the entire electorate.

So, the law of large numbers assures us that as the sample size increases, the exit poll results will converge towards the expected outcome, providing a more reliable indication of the election results.

Do you know why Casino is mostly in profits? 😂

A casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins.

Precaution:-

There is always a chance that the actual result will be very different from the expected value, even with a large number of trials. For example, if a coin is flipped 1,000 times, it is still possible to get 600 heads and 400 tails, even though the expected value is 500 heads and 500 tails.

The Law of Large Numbers is often mistaken for the belief that past outcomes will affect future events. This is not the case this is the assumption that each event is independent and unaffected by the outcomes of previous events. For example, if a coin has landed on heads for the past 10 flips, the probability of it landing on heads again is still 50/50.