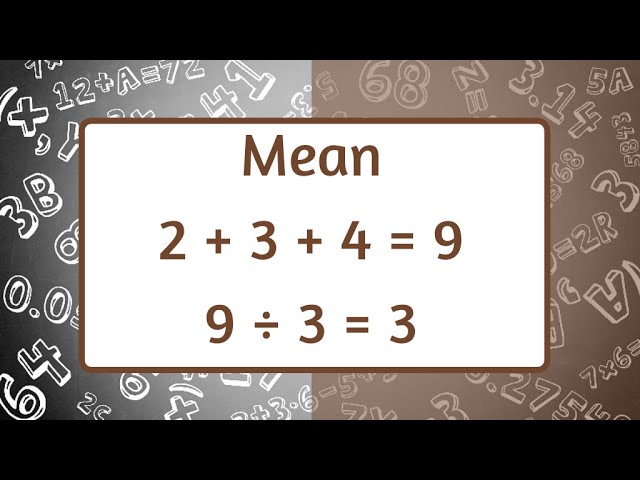
“A number around which a whole data is spread out or the expected value in mathematics.”

What is Mean?

The mean is a way to find the average of a set of numbers.

How to Calculate Mean

1. Add Up All the Numbers: First, you add together all the numbers in the set.
2. Divide by How Many Numbers There Are: Then, you divide the total sum by the number of numbers you added.

Example

Let’s say you have these numbers: 4, 8, and 6.

1. Add the Numbers: 4+8+6=18
2. Divide by the Number of Numbers: There are 3 numbers, so divide by 3. — 18 / 3 = 6

So, the mean (average) of 4, 8, and 6 is 6.

In One Sentence

The mean is the average of a set of numbers, found by adding them all up and then dividing by how many numbers there are.

Do you know we use this measure daily in your life, let me tell you how:-

1. Car Average Fuel Consumption

Imagine you track how much fuel your car uses over several trips to find out its average fuel consumption.

Example:

You drove your car on 5 different trips and recorded the following fuel consumption in liters:

• Trip 1: 6 liters
• Trip 2: 8 liters
• Trip 3: 5 liters
• Trip 4: 7 liters
• Trip 5: 6 liters

To find the average fuel consumption:

1. Add Up All the Fuel Consumption: 6+8+5+7+6=32 Liters
2. Divide by the Number of Trips: There are 5 trips, so divide by 5. ( 32 / 5 = 6.4 )

The average fuel consumption of your car is 6.4 liters per trip.

2. Average Grades

Imagine you want to find out your average grade for a semester by calculating the mean of your grades in different subjects.

Example:

You received the following grades:

• Math: 85
• English: 90
• History: 78
• Science: 88
• Art: 92

To find the average grade:

1. Add Up All the Grades: 85+90+78+88+92=433
2. Divide by the Number of Subjects: There are 5 subjects, so divide by 5. 433/ 5=86.6

Your average grade for the semester is 86, quite how I was always under 60’s-70’s 😂

okay, Let’s see the last example,

3. Average Customer Ratings

Imagine you want to find out the average customer rating for a product based on the ratings given by several customers.

Example:

A product received the following ratings from 7 customers:

• Customer 1: 4 stars
• Customer 2: 5 stars
• Customer 3: 3 stars
• Customer 4: 4 stars
• Customer 5: 5 stars
• Customer 6: 4 stars
• Customer 7: 3 stars

To find the average customer rating:

1. Add Up All the Ratings: 4+5+3+4+5+4+3=28
2. Divide by the Number of Customers: There are 7 customers, so divide 28/7 = 4 Stars.
3. The average customer rating is 4 stars. — Okay, Let’s go and Eat there, 4 is good. — They deserve it.

Well, this is basic maths but now let’s dive into the real world.

To be honest, we can’t count the use cases of Mean because it’s everywhere. But Let me try:-

1) Measure of Central Tendency

• Definition: The mean provides a measure of the central value of a data set.
• Importance: It gives a single value that summarizes the entire data set, helping to understand where most data points are located.

Scenario: Average Daily Steps

Example:

Imagine you tracked the number of steps you took each day for a week, and here are your results:

• Monday: 5,000 steps
• Tuesday: 7,500 steps
• Wednesday: 6,000 steps
• Thursday: 8,000 steps
• Friday: 10,000 steps
• Saturday: 12,000 steps
• Sunday: 9,500 steps

To find the mean (average) number of steps you took per day, you sum up all the steps and divide by the number of days:

Insight:

• The mean number of steps you took per day is approximately 8,285.71.
• This single value summarizes your entire week’s activity, showing that on average, you took about 8,286 steps each day.
• Understanding this helps you know that most of your daily steps were around 8,286, which can help you set goals or assess your physical activity level.

2) Comparing Groups:

• Scenario: We want to compare the performance of two Samples.
• Example: If the average score in Sample A is 80 and in Sample B is 70, you can easily see that, on average, Sample A performed better.

Product Customer Satisfaction

Scenario: A company wants to compare customer satisfaction ratings for two different products.

Data: Customer satisfaction ratings for Product X and Product Y.

• Product X: [4.2, 4.5, 4.0, 4.8, 4.3]
• Product Y: [3.8, 4.0, 3.9, 4.1, 4.2]

Calculation: Calculate the mean customer satisfaction rating for each product.

• Mean Satisfaction for Product X: 4.2+4.5+4.0+4.8+4.35=21.85=4.36
• Mean Satisfaction for Product Y: 3.8+4.0+3.9+4.1+4.25=20.05=4.00

Insight: Product X has a higher average customer satisfaction rating compared to Product Y. This could indicate that customers prefer Product X, and the company might investigate what aspects of Product X are driving higher satisfaction.

3) Identifying Trends:

• Scenario: You track the company’s monthly marketing expenses over a year.
• Example: If your company’s monthly expense is $2,000, you can plan the company’s budget accordingly and identify if there are any months where your company spends significantly more or less than the average.

4) Foundation for Other Statistical Measures

• Variance and Standard Deviation: The mean is essential for calculating the variance and standard deviation, which measure the spread or dispersion of a data set.

5) Baseline Comparison

• Definition: The mean serves as a baseline for comparing other statistical measures.
• Importance: It helps in understanding whether a new observation or prediction is above or below average.
• Example: In anomaly detection, comparing a value to the mean can help identify outliers.

6) Feature Engineering

• Definition: The process of creating new features from existing data.
• Importance: Mean values can be used to create new features that capture the average behavior of a variable over time or across categories.

7) Handling Missing Data:

• Scenario: Your dataset has missing values.
• Example: Replacing missing values with the mean is a simple and effective method to ensure the dataset remains complete for analysis and modeling.

Lastly, I said It’s a best guess for me always, Let me prove it to you.

Assuming you do not anything about Machine Learning or Forecasting models.

• Scenario: Suppose you have to predict the Tomorrow’s Temperature based on temperature recorded over a week: 70°F, 72°F, 68°F, 71°F, 69°F, 75°F, and 73°F.
• Calculation: Add all the temperatures and divide by the number of days.

• The Best Guess would be71.1°F. It’s as simple.

Note: Mean is the most common measure of central tendency but it has a huge downside because it is easily affected by outliers — which value is significantly greater than other values in the data set.

Let me give you an example,

I was sitting in the bar and enjoying my beer. To everyone’s surprise, Elon Musk walks in. I think he wants some drink after openAI suing almost backfired him 😂

I can now say that the average income status of all customers in the bar, including myself, are now in billions.

A perfect example of how to lie with statistics. Be careful while using average, it can be mean to you 😆

In short, Outliers can wreck your model.

Now, As a Statistician, you need to come up with a substitute for the value of Elon Musk’s Salary — Your expertise should lie in using the right value among Mean, Median, MAE, or Mode. In this case, Mean will be sensitive to Outliers, hence not a good choice to Impute the value.

Let’s Imagine, one more example:-

Example: Monthly Salary in a Small Company

Imagine a small company with the following monthly salaries for its 7 employees (in dollars):

• Employee 1: $3,000
• Employee 2: $3,500
• Employee 3: $4,000
• Employee 4: $4,500
• Employee 5: $5,000
• Employee 6: $5,500
• ElonMusk 7: $50,000 (CEO)

Calculation of Mean:

1. The sum of all salaries

2. Number of employees: 7

3. Mean Salary:

Insight:

• The mean salary is approximately $10,786.
• However, this value is heavily skewed by the CEO’s salary of $50,000.

Removing the Outlier:

Let’s see what happens if we remove the outlier (CEO’s salary).

Salaries without the CEO:

• $3,000
• $3,500
• $4,000
• $4,500
• $5,000
• $5,500

1. Sum of salaries without CEO:

2. Number of employees (excluding CEO): 6

3. Mean salary without CEO:

Comparison:

• With Outlier (CEO): Mean salary ≈ $10,786
• Without Outlier (CEO): Mean salary ≈ $4,250

Conclusion: The outlier (CEO’s salary) significantly increases the mean, demonstrating the mean’s sensitivity to outliers. This example shows how a single extreme value can distort the average, making it less representative of the typical value in the data set

Hakuna Matata — Outliers will affect this sum. E.g. a larger positive value than the other values will make the sum large enough so that the mean will also be slightly larger. For a very small value, the mean will also become a bit smaller. Hence the presence of only one outlier can largely affect the mean.

Which measure is the best?

There is no best, but using only one is definitely worst!

How does Python calculate:-

# Using Numpy
import numpy as np
# Create an array of employee salaries
salaries = np.array([3000, 3500, 4000, 4500, 5000, 5500, 50000])
# Calculate the mean salary
mean_salary = np.mean(salaries)
print(f"Mean salary with outlier: {mean_salary}")

# Using Pandas
import pandas as pd
# Create a DataFrame of employee salaries
data = {'Employee': ['Emp1', 'Emp2', 'Emp3', 'Emp4', 'Emp5', 'Emp6', 'CEO'],
'Salary': [3000, 3500, 4000, 4500, 5000, 5500, 50000]}
df = pd.DataFrame(data)
# Calculate the mean salary
mean_salary = df['Salary'].mean()
print(f"Mean salary with outlier: {mean_salary}")