Median — The Middle Most Term

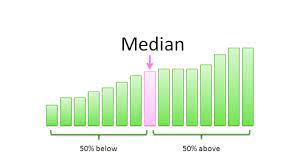
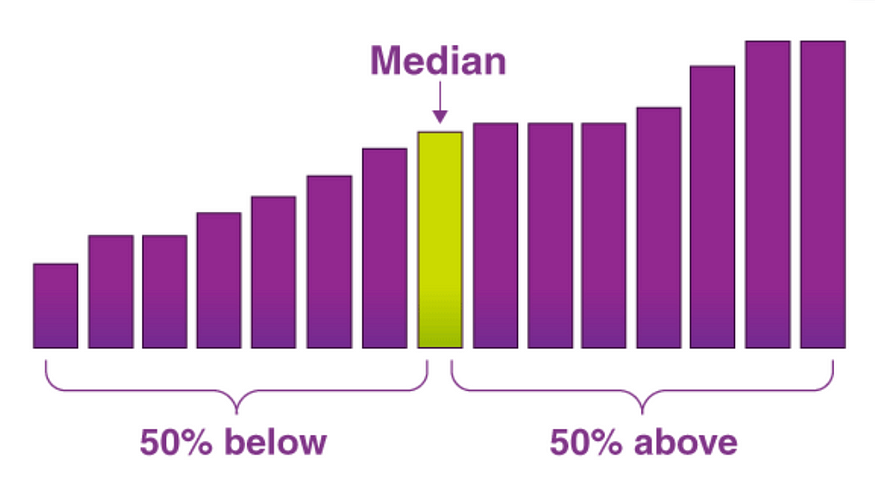
Median

The median is the middle value of a sorted data set; found by ordering all data points and picking out the one in the middle (or if there are two middle numbers, taking the mean of those two numbers).

Let’s find the Median of our data set.

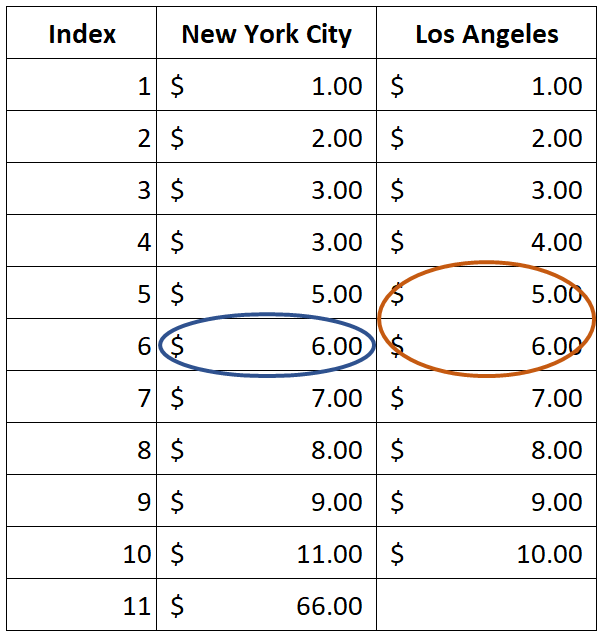
Finding **Median** pizza prices in NY and LA

As you can see, we have a total of 11 observations for NY so the middle position is at the index of 6th which can be calculated as (11+1)/2=6. So the Median of pizza prices in NY is $6.00

What about LA? We have 10 observations in LA so the middle position is between 5th and 6th which can be calculated as (10+1)/2=5.5. So the Median of pizza prices in LA is $5.50

Note: Median is not affected by outliers ($66.00)

Steps to Find the Median

Order the Data: Arrange the data points in ascending (or descending) order.
Determine the Number of Observations (n): Count the total number of data points.
Find the Median Position:

Do you How I did it my primary School:-

Start crossing the number from Right and then Left one by one and you will be left with median only. ✌️

Lets see some of the uses cases in Data Science:-

1. Handling Skewed Data & Outlier Detection

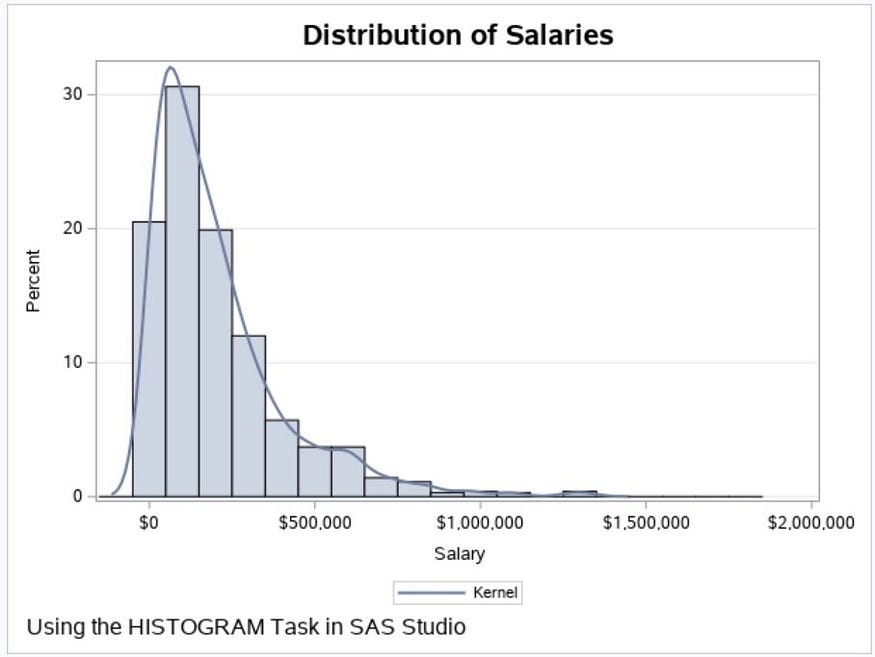
In datasets with skewed distributions, the mean can be misleading due to the influence of outliers and since the median is not affected by outliers, it can be used to detect anomalies in the data. The median provides a better central tendency measure.

Example: Income data often has a long right tail ( Outliers ) due to a few individuals earning significantly more than the rest. The median income gives a better representation of a typical individual’s earnings compared to the mean.

2. Descriptive Statistics

The median is a fundamental descriptive statistic used to summarize data, particularly when reporting on the central tendency of a dataset.

Example: Reporting median test scores in educational assessments to provide a fair measure of student performance.

3. Data Imputation — Most Common

The median is often used to impute missing values in a dataset, especially when the data is skewed.

Example: In a dataset with missing values for household income, the median income can be used to fill in the gaps.

4. Robust Regression Models

In robust regression techniques, the median is used to minimize the impact of outliers on the model.

Example: Median absolute deviation (MAD) is used as a measure of variability when fitting robust linear regression models.

5. Real Estate Analysis

The median price of homes in a region is often reported to provide a more accurate picture of the housing market.

Example: Median home prices are used to gauge affordability and market trends in real estate reports.

In Nutshell, Using the median in these contexts helps to provide a more accurate and reliable measure of central tendency, especially in the presence of skewed data or outliers.

Python Code for computing the Median & Median Imputation

import pandas as pd
# Create a dummy dataset
data = {'Age': [25, 28, 30, 32, 40, 45, 60]}
# Create a Pandas DataFrame
df = pd.DataFrame(data)
# Calculate mean, median, and mode
median_age = df['Age'].median()
print(f"Median Age: {median_age}")


import numpy as np
import pandas as pd
# Example dataset with hard-coded outliers
data = [10, 12, 14, 1000, 15, 20, 30, 1001, 25, 10, 11, 12, 1002]
# Convert to DataFrame
df = pd.DataFrame(data, columns=['values'])
# Hard-coded outliers
outliers = [1000, 1001, 1002]
# Calculate the median of the non-outlier data
non_outliers = [x for x in data if x not in outliers]
median_value = np.median(non_outliers)
# Impute outliers with the median
df['values'] = df['values'].apply(lambda x: median_value if x in outliers else x)
print("Data after imputing outliers:")
print(df)